技術の信頼性で活躍する白石電機工業

Blog 詳細

  • AIを使って発熱体（ヒーター）表面温度を計算してみよう

    2024/10/07 白石電機の仕事

    世の中各段に進歩したもので、xxxxGPTなど、分からないことを質問すれば回答してくれるAIサイトがいくつも出来ています。あるAIサイトに下記のような質問を投げかけてみた。

    「1000℃の炉内温度で炭化珪素発熱体を使っています。表面負荷密度が \( 6\mathrm{W/cm^2} \) であれば、発熱体表面温度が何度になるか計算したいので、エクセルのVBAを作成してください。放射率、発熱体表面負荷密度、炉内温度はセルに入力、計算結果もセルに出力してください。」

    で、下記のように回答頂きました。

    ⇓ AI回答ここから ⇓

    炭化珪素発熱体の表面温度を計算するためのExcel VBAコードを以下に示します。式は、ステファン・ボルツマンの法則を用いて放射エネルギーから表面温度を計算します。

    次の項目をセルに入力します。

    • 放射率 (セルA1)
    • 発熱体の表面負荷密度 (\( \mathrm{W/cm^2} \)、セルA2)
    • 炉内温度 (℃、セルA3)
    • 計算結果はセルA4に表示されるようにします。

    Excel VBAコード

    Sub CalcSurfaceTemperature()
    ' 定数の設定
    Const sigma As Double = 5.670374419E-08 ' ステファン・ボルツマン定数 (W/m2K?)
    
    ' セルから値を取得
    Dim emissivity As Double
    Dim surfaceLoadDensity As Double
    Dim furnaceTemperature As Double
    Dim surfaceTemperature As Double
    
    emissivity = Range("A1").Value ' 放射率
    surfaceLoadDensity = Range("A2").Value * 10000 ' W/cm2 to W/m2 に変換
    furnaceTemperature = Range("A3").Value + 273.15 ' ℃ to K に変換

    ' 表面温度の計算
    surfaceTemperature = ((surfaceLoadDensity / (emissivity * sigma)) + furnaceTemperature ^ 4) ^ 0.25
    
    ' 結果をセルに出力（Kから℃に変換）
    Range("A4").Value = surfaceTemperature - 273.15
End Sub

    使用方法

    1. VBAエディタを開き、新しいモジュールを作成します。
    2. 上記のコードをモジュールにコピー＆ペーストします。
    3. 任意のセル（A1、A2、A3）に放射率、表面負荷密度、炉内温度を入力し、マクロを実行します。
    4. 計算結果がセルA4に表示されます。

    このコードでは、放射率や他のパラメータを自由に入力して表面温度を計算することができます。

    ⇑ AI回答ここまで ⇑

    補足

    1. エクセルのVBAを使うには「ファイル」=>「オプション」=>「リボンのユーザー設定」=>「メイン タブ」の「開発」にチェックを入れる必要があります。
    2. VBAエディタを開くには「開発」タブの「Visual Basic」をクリックします。
    3. 標準モジュールの挿入は「挿入」=>「標準モジュール」の順でクリックします。
    4. ファイルを保存する際、「Excel マクロ有効ブック(*.xlsm)」として保存する必要があります。

    計算結果

    AIが作成したVBAの計算結果

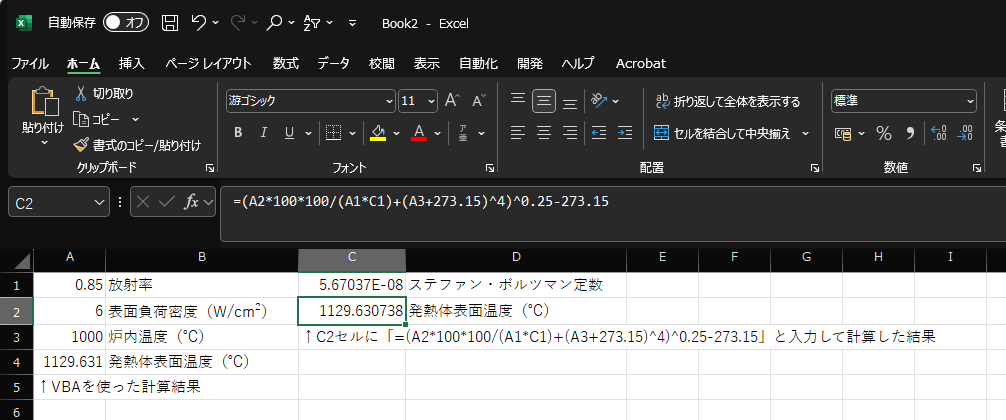
    AIが教えてくれたVBAを実行した結果が上の画像です。B列やC列、5行目にコメントなどを記入したのは私です。セルC2に表示されている値は画像にある計算式を入力して同じ条件で表面温度を計算した値です。当然ながらVBAで計算した結果と同じになっています。

    別にAIを使わなくとも、普通に計算できるわけですがイロイロと面白いのでやってみた次第です。このようなマクロなら数秒から数十秒程度で作ってくれます。

    解説

    せっかくなので一応計算の根拠を解説しておきます。

    発熱体の表面温度を求めるには、表面負荷密度\( q \)と放射率\( \epsilon \)を考慮した熱放射の方程式を使用します。ステファン＝ボルツマンの法則に基づき、発熱体の表面温度\( T_s \)を次のように表すことができます。

    \[ q = \epsilon \sigma ( T_s^{4} – T_a^{4} ) \]

    • \( q: \) 表面負荷密度 \( \mathrm{(W/m^2)} \)
    • \( \epsilon: \) 発熱体の放射率(0.7から0.9の間程度)
    • \( \sigma: \) ステファン・ボルツマン定数 \( 5.67 \times 10^{-8} \mathrm{W/m^{2}K^{4}} \)
    • \( T_s: \) 発熱体表面温度 \( \mathrm{(K)} \)
    • \( T_a: \) 周囲温度 \( \mathrm{(K)} \)

    上の式を \( T_s= \) の式に変形します。

    \[ T_s = \sqrt[4]{\frac{q}{\epsilon \sigma} + T_a^{4}} \]

    この式を解けば発熱体表面温度を求めることが出来ます。

    C2セルに入力した計算式は表面負荷密度 \( \mathrm{W/cm^2} \) を \( \mathrm{W/m^2} \) に、℃をケルビン \( \mathrm{K} \) に換算した式を入力しております。下記にその式を張り付けておきますので、活用されるのであればしてください。

    =(A2*100*100/(A1*C1)+(A3+273.15)^4)^0.25-273.15

    まぁ結論として、ワザワザVBAを使わなくても良さそうな計算ではありますが、AIを使ってみるのも面白いというお話でした。又、このくらいのVBAであれば簡単なので、AIに作ってもらったVBAを元に勉強を始めるのも良いかもですね。知らんけど。。。

    表面負荷密度

    最後に「表面負荷密度」にも触れておきましょう。「表面負荷密度」とは、発熱体の単位面積当たりの電力（発熱量）です。単位は \( \mathrm{W/cm^2} \) で表されることが多いです。（上記VBAは \( \mathrm{W/m^2} \) で計算しています。）他の呼び方として「ワット密度」や「電力密度」と言われることもあります。

    先の計算をするとわかるように、この「表面負荷密度」が高くなるほど、発熱体表面温度も高くなっていきます。従いまして、発熱体の寿命と密接に関係してきます。発熱体の種類により適正な値があるので、発熱体の設計をする際には重要な検討項目になります。こちらは各種発熱体メーカー様がカタログなどに記載されていますので、そちらをご参照ください。

    某発熱体メーカー様のカタログに記載されている炉内温度、発熱体表面温度、表面負荷密度の関係をグラフにされているものと、上記数式を使って計算した結果を比較したところ、ほぼ一致していることも確認しました。

    注意事項として、今回紹介した計算は比較的高温（敢えて温度は書かないですが。）な電気炉に対して有効な計算になります。比較的低温で尚且つ風速があるような場合は、対流による熱伝達も考慮した計算が必要です。

    一番上の画像は未来の白石電機工業（株）をAIが予想し、描いてもらったもの。下はAIに設計してもらった電気炉です。🤭

    AIが設計した電気炉

    MathJaxを使えるようにしてもらい、数式を記入出来るようになりましたが、少々面倒ですな。😑

    中嶋

戻る